Encoding information from 2D views of an object into a 3D representation is crucial for generalized 3D feature extraction and learning. Such features then enable various 3D applications, including reconstruction and generation. We propose GOEmbed: Gradient Origin Embeddings that encodes input 2D images into any 3D representation, without requiring a pre-trained image feature extractor; unlike typical prior approaches in which input images are either encoded using 2D features extracted from large pre-trained models, or customized features are designed to handle different 3D representations; or worse, encoders may not yet be available for specialized 3D neural representations such as MLPs and Hash-grids. We extensively evaluate our proposed general-purpose GOEmbed under different experimental settings on the OmniObject3D benchmark. First, we evaluate how well the mechanism compares against prior encoding mechanisms on multiple 3D representations using an illustrative experiment called Plenoptic-Encoding. Second, the efficacy of the GOEmbed mechanism is further demonstrated by achieving a new SOTA FID of 22.12 on the OmniObject3D generation task using a combination of GOEmbed and DFM (Diffusion with Forward Models), which we call GOEmbedFusion. Finally, we evaluate how the GOEmbed mechanism bolsters sparse-view 3D reconstruction pipelines.
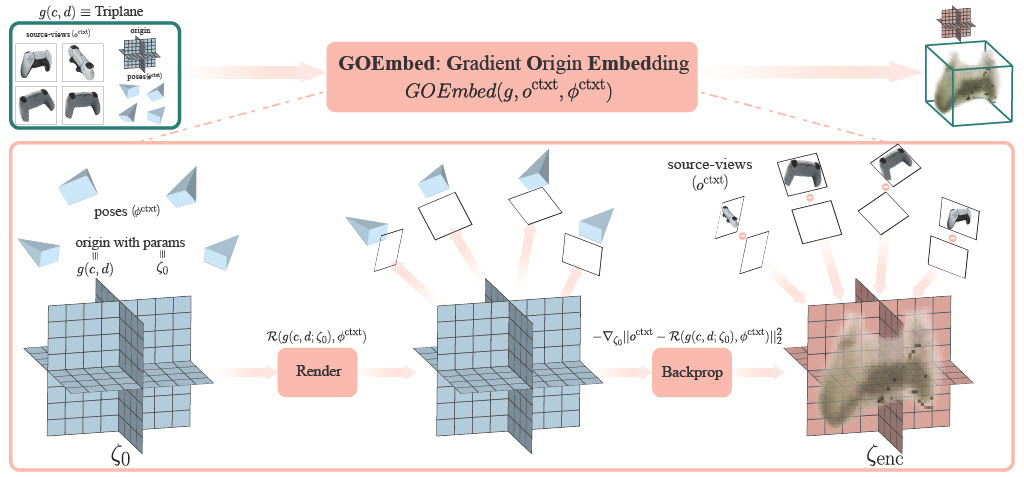
Didactic illustration of the GOEmbed mechanism. We demonstrate the mechanism here using the Triplane representation for \(g(c, d)\), but note that this can be applied to other representations as well. The GOEmbed mechanism consists of two steps. First we render the origin \(\zeta_0\) from the context-poses \(\phi^\text{ctxt}\) into almost blank renders. Then, we compute the gradient of the MSE between the renders and the source-views \(o^\text{ctxt}\) wrt. the origin \(\zeta_0\) which gives us the GOEmbeddings \(\zeta_\text{enc}\).
We propose Gradient Origin Embeddings (GOEmbed), where we define the encodings of the observations as the gradient of the log-likelihood of the observations under the differentiable \(\texttt{forward}\) operation. Without loss of generality, assuming that \(\zeta\) are the parameters of the \(g\) function (i.e. the features/weights of the 3D Radiance-Field), \(\mathcal{R}\) is the differntiable render (\( \texttt{forward} \)) functional and \(\zeta_0\) denotes the origin (zero parameters), we define the encodings \(\zeta_\text{enc}\) (fig. above) as follows: \begin{align} \zeta_\text{enc} &:= GOEmbed(g, o^\text{ctxt}, \phi^\text{ctxt}) \nonumber \\ &\boxed{:= -\nabla_{\zeta_0}||o^\text{ctxt} - \mathcal{R}(g(c, d; \zeta_0), \phi^\text{ctxt})||^2_2.} \label{eq:goembed} \end{align} As done usually, we estimate the log-likehood by the mean squared error and note that the encoding function \(GOEmbed\) backpropagates through the differentiable forward functional \(\mathcal{R}\). These encodings can handle single, or multiple source views by design, and can be used with any 3D representation \(g\). We minimise the following loss function: \begin{align} \mathcal{L}^\text{GOEmbed}(o^\text{ctxt}, o^\text{trgt}) :&= ||o^\text{ctxt} - \hat{o}^\text{ctxt} ||^2_2 + ||o^\text{trgt} - \hat{o}^\text{trgt} ||^2_2 \nonumber \\ \text{where, } \hat{o} &= \mathcal{R}(g(c, d; \zeta_\text{enc}), \phi). \end{align} for maximising the information content in the encodings \(\zeta_\text{enc}\). Here, \(\phi^\text{ctxt}\) are the camera parameters of the context views used for encoding while \(\phi^\text{trgt}\) are the parameters for some target views of the same scene but different from the source ones. Intuitively, we repurpose the backward pass of the rendering functional to encode the information in the source views \(o^\text{ctxt}\) into the parameters of the 3D scene representation \(\zeta\). Thus, as long as a mathematically differentiable rendering operator is possible on it, any 3D scene representation can be encoded using our GOEmbed encoder.
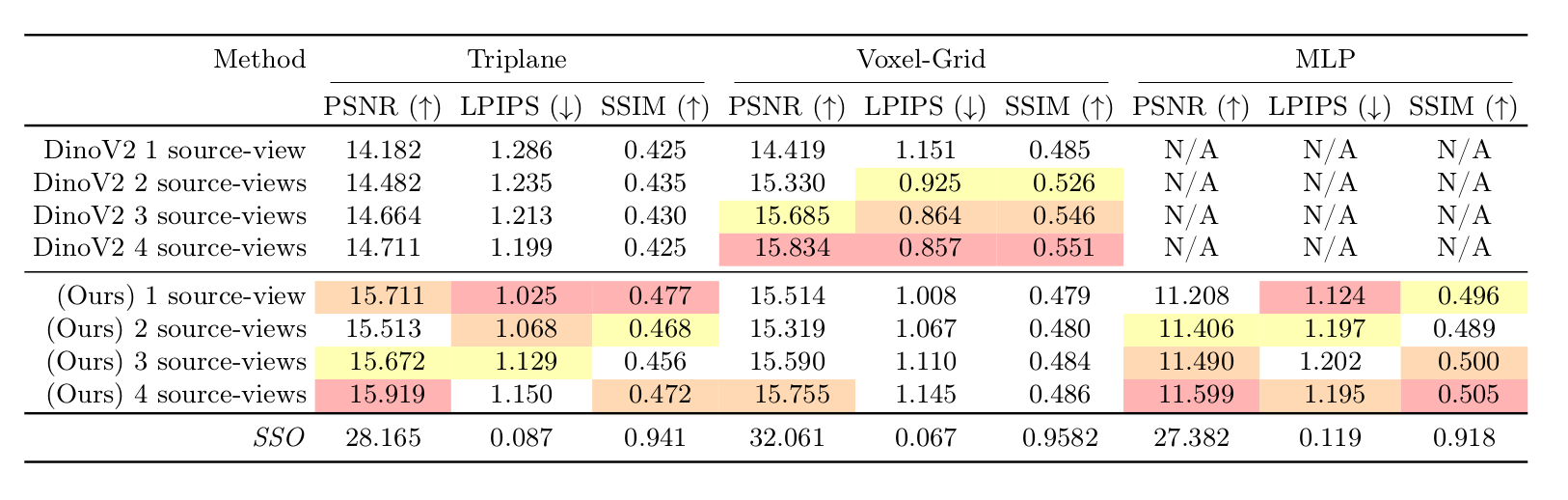
To evaluate the information transfer from the source views to the encoded 3D representation, we train the standalone GOEmbed component on its own before using it in different contexts. Specifically, given the dataset \(D = \lbrace(\mathcal{I}_i^j, \phi_i^j) | i \in [1, N] \text{ and } j \in [1, C]\rbrace\) of \(N\) 3D scenes where each scene contains \(C\) images and camera parameters, we define the Plenoptic Encoding as a mechanism which encodes \(k\) source views and camera parameters, of a certain 3D scene, into the representation \(g\) (whose parameters are \(\zeta\)). The encoded scene representation should be such that the rendered views from the same source cameras, and some \(l\) different target cameras, should be as close as possible to the G.T. images \(\mathcal{I}\), i.e., the PlenopticEncoder \(PE: \mathbb{R}^{k \times h \times w \times c} \times \mathbb{R}^{k \times 4 \times 4} \rightarrow \mathbb{R}^{(k + l) \times h \times w \times c}\) should minimize the following mean squared error objective: \begin{align} \mathcal{L}^\text{PE-MSE} &:= \mathbb{E}_{(\mathcal{I}, \phi) \sim D}\| \mathcal{I} - PE(\mathcal{I}, \phi) \|^2_2 \nonumber. % \\ % \text{where, } \nonumber \\ % PA(\mathcal{I}, \phi) &:= \mathcal{R}(g, \phi; GOEn(g, \mathcal{R}, \mathcal{I}, \phi)). \end{align} Although this experimental setup is quite similar to typical MVS/NVS or 3D reconstruction or 3D prior learning setups, in form and essence; we note here that the plenoptic encoder \(PE\) is neither targeted to do Multi-View Stereo nor 3D reconstruction. To set the correct expectations, we note that the main and the only goal here is to evaluate how much information is transferred from the 2D images to the chosen 3D representation. We evaluate the GOEmbed encodings on three different 3D Radiance-Field representations, \(g\), namely Triplanes, Feature-Voxel grids and MLPs and compare them to cost-volume like approaches where possible.
Plenoptic Encoding Quantitative Evaluation. PSNR(\(\uparrow\)), LPIPS(\(\downarrow\)) and SSIM(\(\uparrow\)) reported on three different representations of the 3D Radiance-Field \(g\), namely, Triplanes, Voxel-Grids and MLPs. All the metrics are evaluated for target views (different from the source views) against the G.T. mesh renders from the dataset. The SSO (Single Scene Overfitting) scores denote the case of individually fitting the representations to the 3D scenes.

Plenoptic Encoding Qualitative Evaluation. The rows MLP, Triplane and Voxel-grid show the renders of the GOEmbed encoded representations from the target-view respectively. The colour-coded columns demonstrate the effect of varying the number-of-source views (1, 2, 3, 4) used in the GOEmbed encoding. The SSO column shows the target render of the single-scene-overfitted representation while the G.T. column shows the mesh-render from the dataset (repeated for clarity).
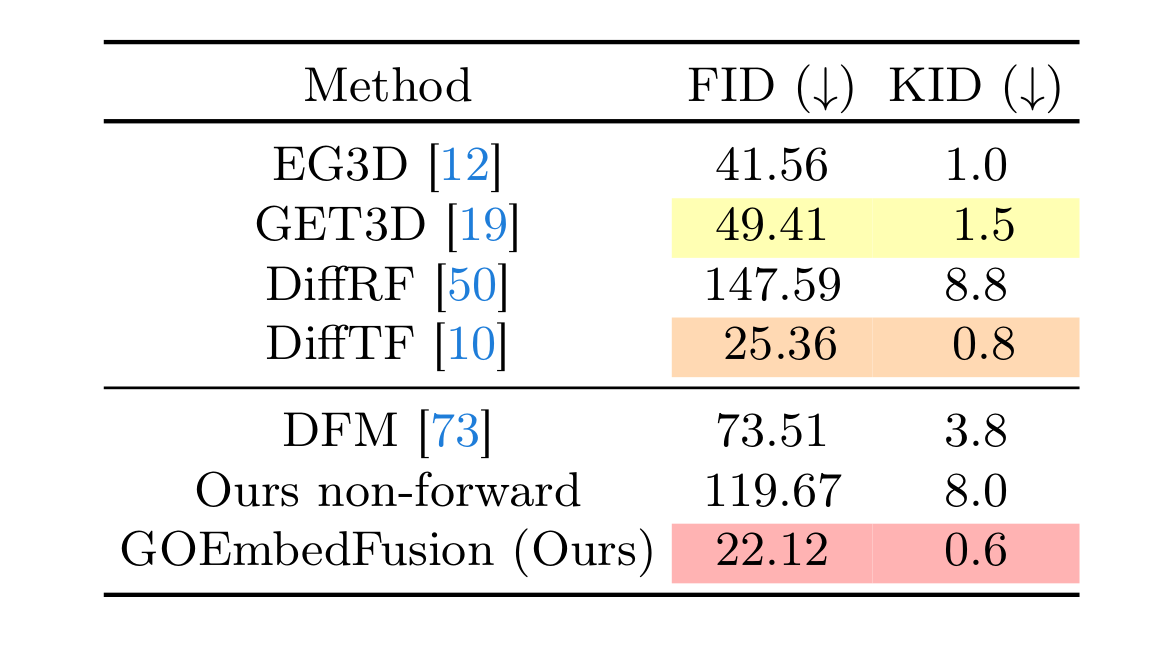
3D Generation Quantitative Evaluation. FID(\(\downarrow\)) and KID(\(\downarrow\)) scores on the OmniObject3D dataset comparing our GOEmbedFusion with GAN baselines EG3D, and GET3D; with the non-forward diffusion baselines DiffRF, DiffTF, and Our non-forward diffusion baseline; and, with the DFM (Diffusion with Forward Model).
DFM
Ours non-forward
DiffTF
GOEmbedFusion (Ours)
3D Generation Qualitative Evaluation. 3D samples generated by our GOEmbedFusion compared to the prior GAN, and Diffusion based baselines. In case of DFM, we perform their vanilla autoregressive sampling procedure to generate the 3D samples. Since, the forward diffusion model is based on the Pixel-NeRF architecture, and since OmniObject3D dataset has random camera locations, the generated videos do not form a smooth closed-loop trajectory around the object. Apart from this, as we can notice, the generated samples are not perfectly 3D-view consistent. Although Ours non-forward samples are 3D-view consistent, they are not visually appealing and have noise-artifacts. Finally, compared to the DiffTF samples, our proposed GOEmbedFusion samples have distinctly sharp appearance and perfect 3D-view consistency. We set the new state-of-the-art FID of 22.12 on the OmniObject3D generation benchmark as opposed to the prior score of 25.36 as obtained by DiffTF.
3D reconstruction Quantitative Evaluation. PSNR(\(\uparrow\)), LPIPS(\(\downarrow\)) and SSIM(\(\downarrow\)) of our GOEmbed reconstruction model, and GOEmbedFusion's ``pseudo''-deterministic 3D reconstruction output compared to LRM baselines. We again include the SSO (Single Scene Overfitting) here for comparison.
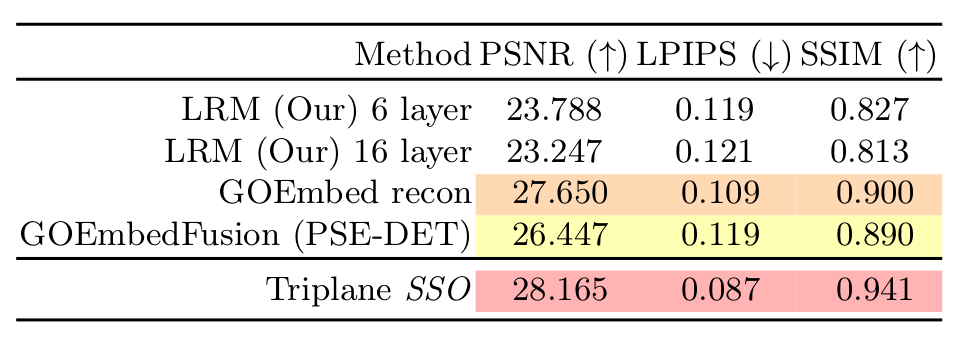
3D reconstruction Qualitative Evaluation. Here we show the 360\(^{\circ}\) rotating videos of the 3D reconstructed scenes from the OmniObject3D dataset. As visible, the LRM 16 and LRM 6 layers models don't have much difference in the qualitative results. However, our proposed GOEmbed recon method shows better results in terms of the overall look and feel, and the spatio-temporal consistency. The LRM reconstructions seem to have the presence of checkerboard-like artifacts while GOEmbed reconstructions are free from such artifacts.
@inproceedings{karnewar2024goembed,
title={{GOEmbed}: Gradient Origin Embeddings for Representation Agnostic 3D Feature Learning},
author={Karnewar, Animesh and Vedaldi, Andrea and Shapovalov, Roman and Monnier, Tom and Mitra, Niloy J and Novotny, David},
booktitle={Proceedings of the IEEE/CVF European Conference on Computer Vision},
year={2024}
}

Animesh and Niloy were partially funded by the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 956585. This research has also been supported by MetaAI and the UCL AI Centre.